|
THERMISTOR TEMPERATURE MEASUREMENT (°C)
The following instruNet hardware supports Thermistor temperature measurements with the help of one user-supplied external shunt resistor:
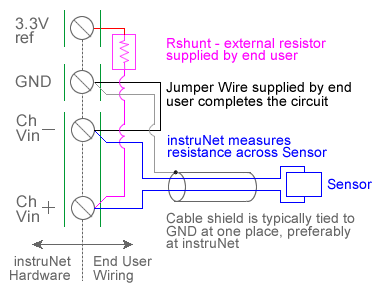
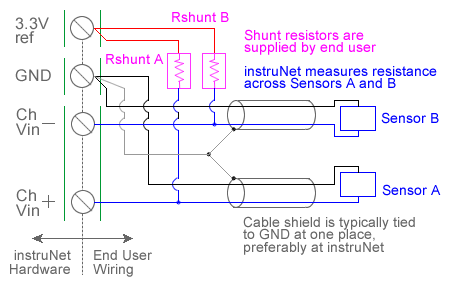
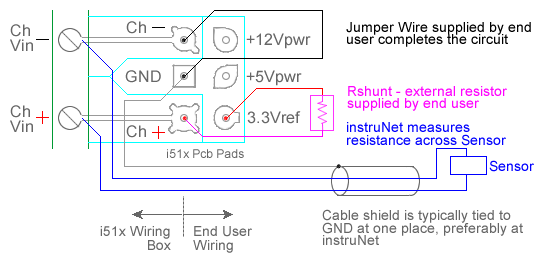
For quick setup instructions, click here. Thermistors are two wire devices who's resistance varies with temperature in a known fashion, often accurate to ± 0.2°C. The instruNet thermistor measurement feature supports ysi-Omega 100Ω to 1MΩ 4xxxx or 4xx series thermistors (not to be confused with instruNet i4xx cards) between the temperatures of -80°C to 250°C. Also, instruNet can measure temperatures from other types of positive and negative thermistors, provided that the end user specifies their Steinhart & Hart Coefficients (click here for details). When Thermistor is selected in the Sensor popup menu, instruNet assumes a thermistor is connected as shown in the above illustrations, and subsequently returns the thermistor temperature in degrees C units after applying a Steinhart & Hart resistance-to-temperature conversion. To do temperature measurement using an thermistor, you must wire your sensor per the above diagram and then set up your software via the Interview process (started after selecting sensor type in Channel Setup dialog) or by manually running through the below steps: 1. Set the Sensor field in the Hardware settings area to Thermistor. This will cause a series of dialog boxes to appear, asking the user several questions about the thermistor type (i.e. resistance at 25°C), shunt resistor value, and excitation voltage. It recommends a shunt resistor based on the thermistor in use and the temperature range of interest 1, 3, 6. In many cases, the recommended values work the best. Based on the responses to these questions, instruNet loads the following fields in the Constants setting group:
instruNet also sets the Measurement Min/Max fields in the Hardware settings area. The smaller the temperature range, the better the accuracy; therefore one should not
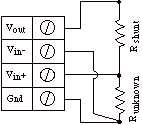
make the specified range unnecessarily large. If you want to run through the dialog box interview again, press the Interview button. If you want to manually set any of the fields in the Constants settings group, do the interview, and then set them to your liking, after selecting Constants in the Settings popup. 2. Wire your thermistor per the above figure. Click here if you need more guidance setting up the software, and click here if the measured value is not correct. 5, 10. To reduce noise, 0.001 seconds of integration is often helpful (i.e. set the Integrate field in the Hardware setting area to 0.001). If you want a detailed report on your setup, press the Sensor Report button in the Channel Setup dialog. Measuring a thermistor temperature from an electrical point of view involves a voltage divider circuit. This uses a shunt resistor of known value and a reference voltage across the shunt resistor and thermistor, as illustrated above. The voltage across the thermistor is measured between the instruNet Vin+ and Vin- input terminals while the excitation voltage for the divider is supplied by the instruNet. instruNet calculates the thermistor resistance using the following equation:
R_therm (ohms) = resistance across thermistor The a, b, and c constants in the above equation are a function of 3 points in the resistance-to-temperature table, and are calculated by instruNet software after the user completes a short dialog box interview. These parameters are sometimes referred to as "Steinhart & Hart Coefficients" or "Steinhart & Hart Parameters". Also, these a/b/c parameters are sometimes referred to as A/B/C (capital letters) in thermistor literature. Setting Up A Non Ysi/Omega 4xxxx or 4xx Series Thermistor If you want to set up a positive or negative thermistor that is not a Ysi/Omega 4xxxx or 4xx Series Thermistors then one must:
Example:
To minimize "self heating", it is recommended that thermistors operate at less than 100 μWatt. In other words, the energy that is pumped into the thermistor device itself to do the device resistance measurement, which causes the device to heat up a little, should be ≤ 0.0001 Watts. For example, a 2252 ohm thermistor that measures temperatures in the 0 to 70°C range with a 3.3V excitation voltage (thermistor varies between 394.5 and 7355 Ω) and 10KΩ ohm shunt resistor would see 37μW at 70°C; as noted below:
Current (Amps) = Volts / Resistance = 3.3V / [10000 + 394.5] = 0.31mA In this case, the voltage across the thermistor varies from 122mV to 1.45V as the resistance across the device varied from 394 to 7355 ohms; therefore, an input Voltage measure range of 0 to 2.5V would suffice. For recommended shunt resistors, click here. The maximum thermistor measurement error is the sum of the following component errors:
|